空氣汙染和COVID-19有關?以生物統計進行流行病學研究
流行病學與統計學是看似不同領域卻密切相關的兩個學門,在公共衛生的領域下,流行病學與生物統計學更是堅定穩固且重中之重的要素。本文將帶領讀者跟著研究者的角度,透過觀察、相對比較、整合運用的過程,了解流行病與統計學如何相輔相成,引領公共衛生與流行病防治。
公共衛生是什麼?流行病學在公共衛生中的重要性
引述文化部臺灣大百科全書中,美國學者文士樂(Charles Winslow)對公共衛生的定義:「公共衛生是一種預防疾病、延長壽命、增進身心健康與效能的科學與藝術。透過有組織的社區力量來從事環境衛生、傳染病管制及個人衛生教育;並組織醫護事業,使疾病得以獲得早期診斷與治療,進而發展社會機構,以保證社會上每個人均有足以維持健康的生活水準,使每一位國民都能實現其健康與長壽的天賦權利。」
流行病學是公共衛生學門的核心課程,著重於疾病預防與臨床醫學的創新與突破,與臨床醫學的互動與互補,在這一波 Omicron 疫情的攻防中,針對高風險群篩檢和醫療量能的掌握更是穩固疫情的要素。孟子有云,天時、地利、人和是成功的三要素,流行病學研究主要也是針對人、時、地的觀察、相對比較、整合運用,其中「觀察」更是流行病學的訓練核心。西方醫學兩大預防治療利器為疫苗與抗生素,也是觀察的運用及研發。擠牛奶的小女孩之間的話語:「我不會得天花,因為我已經得過牛痘。」進而促成了疫苗的發明;抗生素為英國科學家弗來明(Alexander Fleming)觀察時的意外發現,在培養細菌的過程中發現黴菌會製造一種成分來消滅細菌,黴菌可以抑制細菌成長,進而發現抗生素。
以上兩種例子凸顯觀察的重要性,不過流行病學注重的不只是個人,還有群體,也就是不只需要注意確診的病患,還需要觀察沒有染病的群體(也就是實驗中的對照組)。臺灣在SARS上的觀察、推理與假說驗證,傳染途徑的探究與相對策略防範,基因感受性、家族聚集及冠狀病毒脫膜理論,並結合COVID-19 棘蛋白(spike protein) 的轉譯特質,提供臺灣防治COVID-19 強而有力的參考基礎。
流行病學的利器:生物統計
綜上所述,流行病學是一門觀察與期望的科學,屬於方法論,而下文中將介紹的「生物統計」則是流行病學研究中的一項工具。工欲善其事,必先利其器,流行病學與生物統計學兩者相輔相成,構成研究中的假說、研究架構與驗證。
生物統計以相當思維核心的中央極限定理來做概要論述[註],生物統計將數據主要呈現為三項特質,包括趨中性、離異性、分布:
1. 趨中性
趨中性是提供給流行病學家數理上的期望值,距離期望值愈近機率愈高。趨中性主要包括:平均數、中位數和眾數,母數分析可以平均數為期望值(對母群分布有所假定,例如常態分布),如果期望值為中位數,基本上可以應用中位數機率學特性 (大於中位數與小於中位數的機率相等)進行推導,因無須對母群有強烈假設,一般設定為無母數分析進行探討。
2. 離異性
如果資料沒有變異也就不需要統計,在方程式與統計迴歸式的差別,就是迴歸式比方程式多了一項殘差值(error term,觀察值與方程式預測線的距離)。而迴歸式中的變異數是每個觀察值與期望值距離平方後加總的平均值,變異數開根號,則為標準差。有相當大比例的統計方法與進階統計研發開拓,主要都是針對變異性的調整,例如流行病學三大特質(人、時、地)的獨立檢定與相關檢定:人體重複量測數據分析的一般線性廣義估計模式 (general linear model-generalized estimating equations, GLM-GEE)、時間序列分析(time series analysis)、地理資訊系統分析(geographic information system, GIS) 等。在一般的檢定方法中,數據量測值之間的獨立性假設需要調整,也需要進行變異數的對應調整評估與進階估計。
3.分布
分布的假定應用中,只要樣本數夠多 (通常以樣本數30左右,樣本t分布與母群z分布趨近),樣本平均數的分布都會趨近常態 (不論原母群分布是否為常態分布,深層分布的探討都是統計進階重要課題)。在母數分析常態分布假設裡面,期望值是平均數,當觀察值與期望值的距離大於1.96個標準差時,機率值(p值)小於0.05,這樣的差距就不是能用機率可以解釋的。
總結以上,流行病學與生物統計的特點皆為觀察與期望的比較,是探討暴露(因)與疾病(果)最為深層的根本,如同卡通《名偵探柯南》,追根究底,探討因果。需注意的是流行病學研究一定有對照組提供對比期望值,比較病患與健康族群暴露勝算的比值 (勝算比),或暴露與未暴露族群的追蹤期間罹病風險的差距(絕對風險)和比值 (相對危險比)。
跟著生統步驟求證!空氣汙染和COVID-19有關嗎?
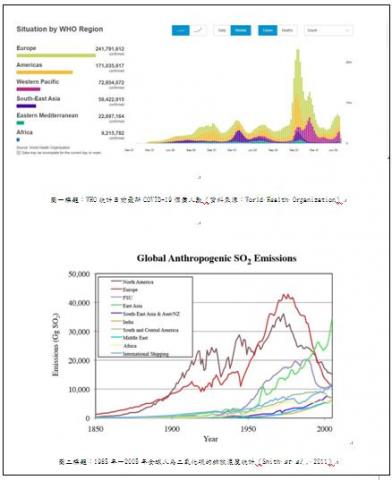
當觀察值遠大於期望值,就是流行病學進一步研究的開始。流行病學為大膽假設的企圖,生物統計則是小心求證的步驟。以傳染病為例,依照世界衛生組織最新統計發生COVID-19個案數,發生個案為歐洲最高,第二為美國,東南亞相對較低 (圖一),依照全球人為二氧化硫(sulphur dioxide, SO2)排放濃度統計(1985年-2005年),可以看到以歐洲累積暴露量最高,美國為第二,東南亞也相對較低 (圖二)。透過觀察,我們可以設定COVID-19與二氧化硫可能具有相關性的假說,接著再運用統計模式解釋二氧化硫差異的可能性,驗證假設。在數理模式推導中,單純二氧化硫和COVID-19的發生可以應相關係數,探討共變的相關性,並考量空氣汙染暴露對疾病短期(立即性)和長期(累積性)效應,及多元因素影響 (例如干擾因子),逐步分析探討:
1. COVID-19 、空氣汙染與相關危險因子的單因子分布/頻率呈現探討,明瞭整體範圍與趨勢,決定分析策略及最佳可能對應統計分析執行。
2.進行 COVID-19 發生與空氣汙染及相關危險因子(干擾因子)的單變項分析及簡單迴歸分析。
3.執行二氧化硫對COVID-19的影響深入探討與評估。
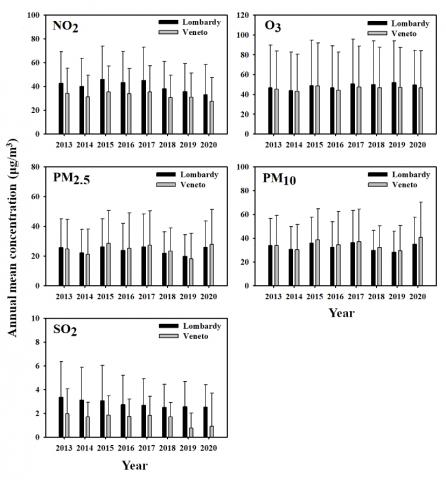
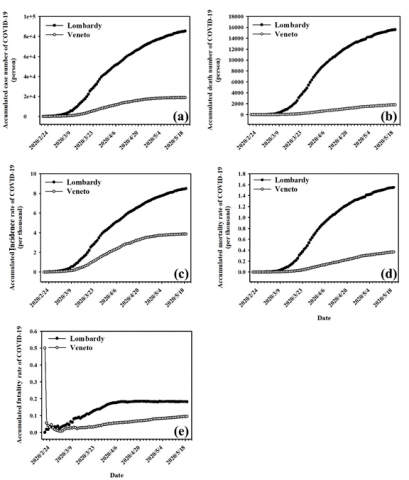
筆者的跨領域研究團隊就針對這個假設與分析方法,在歐洲第一個COVID-19大流行的國家:義大利,選擇義大利北部兩個重要地區的第一波COVID-19傳染流行案例 (圖三),收集倫巴第(Lombardy)和威尼托(Veneto)地區的空氣污染監測數據,分析與探討二氧化硫等空氣污染物對COVID-19發生率與嚴重度(圖四)。結果發現長期暴露在二氧化硫下對COVID-19的影響,比較短期暴露更為顯著,而且無論短期和長期暴露都會增加對COVID-19感染的發生率和致死率。我們的研究結果表明,空氣污染的暴露對於COVID-19大流行具有重大影響。
根據上面這項研究結果,筆者也與中國醫藥大學新藥開發研究中心主任洪士杰日前共同發表動物實驗數據及臨床研究,發現二氧化硫對血管收縮素轉化酶(angiotensin-converting enzyme 2, ACE2)有刺激作用,而ACE2為目前已知導致COVID-19入侵人體的通道。所以,未來研究團隊也會結合臨床研究與國際流行病學相關數據做進一步研究,找出兩者之間的關聯性。
每一個統計分析方法,都有它們擅長探討與優勢之處,在應用時需要確知統計方法的前提與假設,使用適切的統計方法。在數據分析的應用上,善用最佳知識提供訊息參考,並時時思考可能的侷限與突破。
我思故我在,歡迎讀者們對世界探索充滿好奇心,勇於創新、對觀察到的現象問:「為什麼?」,時刻追求探索真相。也歡迎對人類疫病預防、健康福祉與發展促進深耕有興趣的有志青年,一起加入流行病學、生物統計及公共衛生的研究探索行列,創新、助人與永續卓越精進服務,實現健康天賦人權。
延伸閱讀:
Smith, S. J., et al. (2011). Anthropogenic sulfur dioxide emissions: 1850–2005. Atmospheric Chemistry and Physics, 11(3), 1101-1116.
Ho, C. C., et al. (2021). Effects of short-and long-term exposure to atmospheric pollution on COVID-19 risk and fatality: analysis of the first epidemic wave in northern Italy. Environmental research, 199, 111293.
劉士永,公共衛生,文化部臺灣大百科全書,https://nrch.culture.tw/twpedia.aspx?id=3778。
[註]中央極限定理是指給定一個任意分配的母群,每次從中隨機抽取n個樣本,一共抽m次。然後把這m組樣本分別求出平均值。隨著m的增加,這些平均值的在特定的分配下會接近常態分佈。
資料來源:《流行病與統計學─科學月刊》 10/2022 公共衛生學系主任/何文照教授 本校校園公告